
Mit der vorliegenden 25. Ausgabe kommt das Quartl in sein siebtes Jahr. Wird es sein letzter Jahrgang sein? Manches spricht dafür, muss doch der FORTWIHR bekanntlich am 1.9.2000 zum ehemaligen Forschungsverbund mutieren, und die mit seiner rückstandsfreien Entsorgung beauftragten Abdecker stehen womöglich schon Gewehr bei Fuß. Oder wird es doch Rückstände geben? Schließlich bildet sich zumindest der im Lesen zwischen den Zeilen Geübte durchaus ein, im Namenszug KONWIHR des neuen Kompetenznetzwerks für technisch-wissenschaftliches Hochleistungsrechnen in Bayern Bekanntes zu entdecken. Gar Rückstände? Oder nur Ausdruck eines stolz-gesunden Verharrens bei fest verwurzelten Traditionen, selbstverständlich einhergehend mit beherzt-überzeugtem Galopp in die glorreiche Zukunft, gewissermaßen wie beim viel zitierten Laptop und seiner Lebensabschnittsgefährtin Lederhose? Und wie hat man sich überhaupt den Übergang von verbundener bayerischer Forschung zu vernetzter Kompetenz folgerichtig auf das neue Jahr, welches - ich weiß nicht, ob Sie's schon wussten - ja zugleich auch neues Jahrzehnt, -hundert und -tausend bedeuten wird. Auch wenn die Erinnerung an den letzten Millenniumswechsel bei den meisten Lesern nicht mehr ganz taufrisch sein dürfte, so wird einem doch schlagartig bewusst, was für ein Geschenk es ist, in einer derart ereignisreichen Zeit zu leben. Arme Ritter, arme Mönche - keine Verbünde, keine Netzwerke und kein Quartl!
Doch nutzen wir die besinnliche Vorweihnachtszeit, kehren ein (innerlich, selbstredend) und blicken zurück auf sechs Jahre Quartl. Es begann erstaunlicherweise mit der ersten Ausgabe, die zu einigen irritierten Anfragen an unseren seinerzeit noch stellvertretenden Sprecher führte, ob denn der FORTWIHR eigentlich eine seriöse Einrichtung und ernst zu nehmen sei. Nun, der glückliche Besitzer eines Originalexemplars schlägt nach und gelangt angesichts des retrospektiv geradezu devot und stocksteif anmutenden Inhalts eher zu dem Schluss, dass die betreffenden Anrufer schwerlich so richtig ernst genommen werden konnten (was sie übrigens auch nicht wurden). Zum nächsten Meilenstein geriet die Nachlese über die Ausstellungsreihe "Aktuelle Wissenschaft im Deutschen Museum" in der achten Ausgabe (4/1995), mit der, zunächst ganz ungewollt, unser Einstieg ins Sottisengeschäft gelang. Was war geschehen? Wir hatten unsere "Wissenschaftler zum Anfassen", die vier Monate lang Wochenende für Wochenende am FORTWIHR-Stand Flagge gezeigt hatten, lediglich gefragt, ob der Nachbarstand eines befreundeten Verbunds ebenfalls immer besetzt gewesen sei. Das eindeutige Umfrageergebnis (Null aus irgendwas) wurde daraufhin im Quartl mit den Worten "Zunächst wurde der Einsatz von Tarnkappen vermutet, aber als der Rechner gar nicht mehr lief und die Plakate von den Wänden fielen, war klar, dass sich die künstliche Intelligenz nicht anfassen lässt" kommentiert. Es folgten genüssliches Rezitieren, empörte Telefonate und das Zugeständnis des damaligen Sprechers, zukünftig zensorisch tätig zu sein. Es erübrigt sich wohl, über die Heftigkeit seines diesbezüglichen Tuns ein Wort zu verlieren. Soviel sei dennoch gesagt: Obwohl die Toleranzschwelle nicht zuletzt mit Unterstützung des Redaktionsmitglieds Jack Daniel nach Kräften ausgelotet wurde, kam es nur einmal zu einer Intervention - pikanterweise wieder bei einer Nachlese (3/98).
Doch noch kurz zu den Highlights der jüngsten Zeit: Im November outete sich ein weiterer Kanzler einer bayerischen Universität als begeisterter Quartl-Leser, aus ganz ungeahnten Richtungen werde ich immer wieder auf das Quartl angesprochen (was sehr anschaulich den Unterschied zwischen "Auflage" und "Reichweite" einer Zeitschrift verdeutlicht), und einer der Super-Dreadnoughts des FORTWIHR sammelte neulich mit dem Freudschen Versprecher vom "Quatschl" Pluspunkte. Trotzdem gibt es noch Steigerungsmöglichkeiten, einen Anruf aus Berlin zum Beispiel: "Wie war ich, Quartl?"

Unserer gesamten Leserschaft wünscht die Quartl-Redaktion frohe
Weihnachten, wenig Ärger mit Y2K, Knallerbsensträuchern oder Maschendrahtzäunen und ein gutes Neues Jahr(tausend)!
Der Boden, hier als dünne Grenzschicht zwischen Atmosphäre und felsigem Untergrund verstanden, wirkt u.a. auch als Filter, der den Eintrag von Schadstoffen (z.B. von in der Landwirtschaft eingesetzten Pestiziden oder Düngern) behindert. Diese Filterwirkung hängt maßgeblich von zwei Faktoren ab: der Geschwindigkeit, mit der das Transportmedium Wasser durch den Boden fließt, sowie der physiko-chemischen Wechselwirkung der Schadstoffe mit der Bodenmatrix. In diesem Beitrag wird das Transportproblem adressiert. Obwohl natürlich Kontinuumsmodelle für die Vorhersage der Transporteigenschaften von Böden in Abhängigkeit von zu messenden makroskopischen Parametern existieren, erweisen sich diese Voraussagen oft als zu konservativ, speziell in Fällen, wo sich ein Boden im sog. ungesättigten Zustand befindet, der Porenraum also zu vergleichbaren Volumenanteilen mit Wasser und Luft gefüllt ist. Dies impliziert oft ein sensibles Systemverhalten, welches sich als sogenannter "preferential flow" äußert. Wasser- und damit Schadstofftransport findet dann stark lokalisiert und zum Teil um Größenordnungen intensiver statt, als prognostiziert. Um das Verständnis für solche Makrophänomene zu verbessern, versucht man in den Bodenwissenschaften seit neuestem u.a. topologische und geometrische Eigenschaften von Böden in neue Modelle zu integerieren. Der Wunschtraum des "gläsernen Bodens" ist zwar makroskopisch kaum zu realisieren, für kleine Volumina (O(1 cm3)) lassen sich jedoch durch Röntgentomographie digitale Repräsentationen dieser ungewöhnlich komplexen Geometrien erstellen (siehe Abb. 1, Daten: P. Lehmann, ETH Zürich).

Abb. 1: Rekonstruierte Sandbodenprobe: ca. 2 cm3, Auflösung: O(107) Gitterknoten
Unter Verwendung solcher "realen" Geometrien soll nun mittels Simulation versucht werden, die für das makroskopische Transportverhalten relevanten Teilprozesse im Detail zu untersuchen. Im Rahmen des neuen DFG-Projektes MUSKAT (MUlti-SKAlen-Transport in Böden) und in Zusammenarbeit mit dem Institut für terrestrische Ökologie der ETH Zürich wird nun u.a. versucht, aus der numerischen Lösung des durch die Mehrphasenproblematik stark erschwerten transienten Navier-Stokes Problems neue Ansätze für verbesserte makroskopische Modelle abzuleiten. Ein wichtiger "Fingerabdruck" einer Bodenprobe ist ihr hystereseartiges Verhalten bezüglich des stationären Wassergehaltes beim Be- und Entwässern unter Anlegen unterschiedlicher Saugspannungen (sozusagen eine Phasenraumcharakterisierung des Sättigungsverhaltens). Diese Hysterese resultiert aus den unterschiedlichen Benetzungseigenschaften von Wasser und Luft sowie einer Vielzahl von dynamischen Effekten (Blasenbildung, Kapillarphänomene und andere).
Schon die qualitative Rekonstruktion einer solchen Hysterese ist daher ein erster harter Test für den am LS Bauinformatik der TUM entwickelten Simulationskernel FLASH, der auf Lattice-Boltzmann Ansätzen basiert, welche auch im aktuellen FORTWIHR Programm gefördert werden. Diese Feuertaufe ist nun bestanden. Schon bei ersten Testsimulationen mit einer Probe von nur 3/100 cm3 konnten alle charakteristischen Eigenschaften der experimentell aus einem Säulenexperiment erhaltenen Hysterese erstmals für ein Mehrphasen-Navier-Stokes Modell und eine realistische mikroskopische Geometrie reproduziert werden (Abb. 2).
 |
 |
Abb. 2: Experimentelle und simulierte Hysteresekurve einer Mikrobodenprobe
In den Abb. 3.1 bis 3.3 sind unter Verwendung von Isoflächen die Kornverteilung der Simulationsgeometrie, die Phasenverteilung von Restluft nach spontaner Benetzung sowie die residuale Wasserverteilung nach einer Drainage dargestellt.


Abb. 3.2: Restluft nach spontaner Benetzung

Abb. 3.3: Restwasser nach Drainage
Natürlich ist es von hier noch ein weiter Weg bis zur erhofften
quantitativen Übereinstimmung mit dem Experiment, nicht zuletzt aufgrund von
physikalischen Wissenslücken bezüglich der Kontaktwinkelproblematik.
Dennoch sind wir optimistisch, durch
algorithmische Optimierungen und die zur Zeit erfolgende
Portierung des parallelen FLASH Prototyps auf die VPP 700 am LRZ
ein Werkzeug zur Verfügung zu stellen, welches helfen kann, auf dem Weg zum "gläsernen
Boden" ein gutes Stück voranzukommen.
Um in diesem komplexen Prozess Vorhersagen über charakteristische mikro- und mesoskopische Eigenschaften zu treffen ist ein Drei-Skalen-Modell entwickelt worden (Abb. 1).
| Mikroskopisch | Mesoskopisch | Makroskopisch |
|---|---|---|
 |
 |
 |
| Dendriten Mikrostruktur |
Gefüge Kornstruktur | Werkstück Temperatur |
Auf der makroskopischen Skala in Größenordnung des Werkstückes
werden gemittelte Transportgleichungen zur Berechnung des makroskopischen
Wärme- und Stofftransportes verwendet. Auf der mesoskopischen Skala
wird das Kornwachstum simuliert. Auf der mikroskopischen Skala wird schließlich
das Wachstum einzelner Kristalle näherungsweise berechnet und
somit Aussagen über Dendritenabstände, Wachstumsgeschwindigkeiten der
Dendriten, Mikrosegregation und
volumetrischen Feststoffanteil gewonnen. Alle drei Skalen sind
miteinander gekoppelt. So gehen die volumetrischen
Feststoffanteile aus der Mikro- und Mesoskala über die freigesetzte latente
Wärme in das makroskopische Transportproblem ein, auf der anderen Seite
werden die makroskopischen Temperaturdaten als Randbedingungen für
das meso- und das mikroskopische Problem benötigt.
Die Makroskala:
Das einfachste makroskopische Modell für die Verfestigung eines reinen
Stoffes ist ein Mischungsmodell, bei dem mikroskopische
Temperaturschwankungen vernachlässigt werden,



 den Feststoffanteil
bezeichnet. Alternativ dazu kann man die effektive
Wärmeleitfähigkeit aus mikroskopischen Betrachtungen bestimmen;
man erhält dann mit mehr Aufwand eine genauere Approximation.
den Feststoffanteil
bezeichnet. Alternativ dazu kann man die effektive
Wärmeleitfähigkeit aus mikroskopischen Betrachtungen bestimmen;
man erhält dann mit mehr Aufwand eine genauere Approximation.
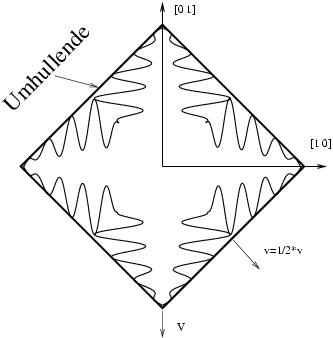
Abb. 2: Mesoskopische Beschreibung eines Korns
Zwischen ihnen bildet sich ein feineres Netzwerk aus sekundären und
tertiären Dendriten aus.
Die Wachstumsgeschwindigkeit bestimmt sich als
Funktion der lokalen Unterkühlung der Dendritenspitzen oder aus dem
mikroskopischen Modell. Um die Wechselwirkung sehr vieler Körner zu untersuchen,
muss die Modellierung eines Korns stark vereinfacht werden.
Die innere
dendritische Struktur wird vernachlässigt, und das Wachstum des Korns wird
bestimmt durch das Wachstum seiner Umhüllenden. Die Umhüllende selbst wird in
guter Näherung als Rechteck beschrieben. Korngrenzen entstehen dann an
den Berührungspunkten der Umhüllenden verschiedener Körner (Abb. 2).
Die Mikroskala:
Auf der Mikroskala wird das Wachstum eines einzelnen Dendriten bestimmt.
Das Kristallwachstum wird dann durch das Stefan-Problem mit
Gibbs-Thomson-Unterkühlung beschrieben.
Die exakte Berechnung des Kristallwachstums ist jedoch immer noch viel zu
aufwendig, da im Idealfall für jeden Gitterpunkt eines Netzes des
makroskopischen Problems das Wachstum des Dendriten berechnet werden
muß. Daher verwenden wir hier eine vergleichsweise grobe
Approximation des Kristalles mit wenigen Parametern, wie z. B. in
Abb. 3 für einen Dendritenarm eines equiaxialen Kristalles skizziert. Aus dieser Approximation lassen
sich bereits wesentliche Parameter der Mikrostruktur ablesen.
 |
 |
Abb. 3: Approximation der Mikrostruktur
Die Berechnung dieses Kristallwachstums beruht auf der Minimierung eines
Energiefunktionals.
Dieses ordnet jedem "zulässigen" Feststoffgebiet
 im Gebiet eine reelle Zahl zu und ist gegeben durch
im Gebiet eine reelle Zahl zu und ist gegeben durch


 . Der zweite und dritte Term
bestrafen Temperaturen oberhalb des Schmelzpunktes in der
Feststoffphase bzw. Temperaturen unterhalb des Schmelzpunktes in der
Flüssigphase. Die Euler-Lagrange-Gleichungen dieses
Optimierungsproblems liefern
für eine feste Funktion gerade die Gibbs-Thomson Bedingung.
. Der zweite und dritte Term
bestrafen Temperaturen oberhalb des Schmelzpunktes in der
Feststoffphase bzw. Temperaturen unterhalb des Schmelzpunktes in der
Flüssigphase. Die Euler-Lagrange-Gleichungen dieses
Optimierungsproblems liefern
für eine feste Funktion gerade die Gibbs-Thomson Bedingung.
Die Kopplung dieser drei Modelle soll es ermöglichen,
mikroskopische und mesoskopische Eigenschaften von Gussstücken
vorherzusagen und Aussagen über optimale Prozessbedingungen zu erhalten.
Es ist noch viel zu tun, wir arbeiten daran.

Ferienakademie im Sarntal: zu den besonderen Attraktionen in diesem Jahr zählte sicherlich der Gesprächsabend "im Doppelpack" mit TU-Präsident Prof. W. A. Herrmann und Ltd. MR H. Kopplinger von der Bayerischen Forschungsstiftung.
Der Einladung folgten der Lehrstuhl für Theoretische Astrophysik der Universität Tübingen, der Lehrstuhl für Graphisch-Interaktive Systeme der Universität Tübingen, die Abteilung Visualisierung und Interaktive Systeme am Institut für Informatik der Universität Stuttgart, der SFB 382 Verfahren und Algorithmen zur Simulation physikalischer Prozesse auf Hochleistungsrechnern (Tübingen und Stuttgart), das Hochleistungsrechenzentrum Stuttgart, der Lehrstuhl für Informatik 9 der FAU Erlangen sowie der SFB 603 Modellbasierte Analyse und Visualisierung komplexer Szenen und Sensordaten (Erlangen). Die gastgebenden Institutionen waren vertreten durch die TUM-Lehrstühle für Höhere und Numerische Mathematik (Prof. Bulirsch), Bauinformatik (Prof. Rank), Flugmechanik und Flugregelung (Prof. Sachs) und Informatik V (Prof. Zenger) sowie durch den Lehrstuhl für Strömungsmechanik der FAU Erlangen-Nürnberg (Prof. Durst).
Neben einem bunt gemischten Vortragsprogramm (siehe Kasten), bereichert und aufgelockert durch zahlreiche Vorführungen am Rechner, bot der Visualisierungstag vor allem Gelegenheit zum Erfahrungsaustausch sowie zur Besichtigung des Flugsimulators am Lehrstuhl für Flugmechanik und Fluregelung. Zu einem weiteren Höhepunkt geriet die Vorführung eines Lern- und Spielprogramms für angehende Piloten von Modellflugzeugen: Prof. Ruders "billigste Doktoranden" präsentierten ihr eifrig vermarktetes, überaus eindrucksvolles Produkt.
| Dies gab's zu hören und sehen: | |||
|---|---|---|---|
| 11.00 | Siegfried Kühner | Bauinformatik, TU | Visualisierung von Windströmungen in und um Bauwerke |
| 11.20 | Martin Vögel | Mathematik, TUM | Dynamik von Robotern und Kraftfahrzeugen: Simulation und 3D Animation |
| 11.40 | Frank Schäfer | LSTM, FAU | Integrated Particle Tracing within a Multiblock Flow Simulation Program: Validation and Application |
| 12.00 | Matthias Hopf | Informatik, Uni S | Hardwarebeschleunigte Volumenfilterung |
| 14.00 | Flugsimulator | Flugmechanik, TUM | Besichtigung, Vorführung, Flugversuche |
| 14.40 | Christof Rezk-Salama | Informatik, FAU | Interaktive Visualisierung von feinen Gefäßstrukturen in MR Daten |
| 15.00 | Daniel Weiskopf | Astrophysik, Uni Tübingen | Texturbasiertes Rendering zur Visualisierung der speziellen Relativitätstheorie |
| 16.00 | Ulrich Hoffmann | Informatik, Uni Tübingen | Klassifizierung und Beleuchtungsberechnung für 3D-Textur basiertes Volume Rendering |
| 16.20 | Peter Breitling | Informatik, TUM | Visualisierung hierarchisch adaptiver Datenstrukturen |
| 16.40 | Hans-Joachim Bungartz | Informatik, TUM | Das Praktikum "Anwendungen der Computergraphik" |
Schließlich war es für einige unserer Gäste auch der erste Besuch in den kargen neuen
Räumlichkeiten der Fakultät für Maschinenwesen der TUM -
da fühlte sich manch einer an klösterliche Askese erinnert.
Der Kurzlehrgang gibt eine Einführung in die numerische Lösung von Strömungs- und Wärmeübertragungsproblemen. In 20 einstündigen Einzelvorlesungen und zusätzlichen Computerdemonstrationen werden die Grundlagen der Finite-Volumen-, der Finite-Differenzen- und der Finite-Elemente-Berechnungsverfahren vermittelt und verschiedene Anwendungsmöglichkeiten vorgestellt.
In den Vorträgen werden alle Schritte von der Diskretisierung über den Einbau der Randbedingungen bis zur gekoppelten Lösung der Erhaltungsgleichungen behandelt. Neben den zugrundeliegenden Ideen werden die gebräuchlichen Approximationsmethoden und Diskretisierungsschemata im Detail beschrieben. Ergänzend zur Erläuterung der Grundgleichungen der Strömungsmechanik wird die Modellierung und numerische Implementierung typischer Phänomene wie Turbulenz oder Wärme- und Stoffübertragung dargestellt.
Um aufzuzeigen, wie die Effizienz der zum Teil sehr aufwendigen Strömungsberechnungen erhöht werden kann, wird die Mehrgittertechnik vorgestellt und eine Einführung in die Diskretisierung mittels dünner Gitter gegeben. Eine besondere Bedeutung kommt in diesem Zusammenhang der Portierung von Strömungsprogrammen auf Hochleistungsrechner (Vektor-, Parallel- und Vektor-Parallelrechner) zu, die aus diesem Grund in einer eigenen Vorlesung behandelt wird. Das Technisch-Wissenschaftliche Hochleistungsrechnen wird vielfach als Voraussetzung dafür angegeben, komplexe dreidimensionale Strömungssimulationen in Rechenzeiten durchzuführen, die für die industrielle Praxis akzeptabel sind. Die Weiterentwicklung und Etablierung dieser Disziplin wird an der Universität Erlangen-Nürnberg von Wissenschaftlern verschiedener Fachrichtungen verfolgt, um Anwendern aus Forschung und Industrie geeignete Hilfsmittel zur Verfügung stellen zu können. Die aus diesen Arbeiten resultierenden Ergebnisse und der aktuelle Wissensstand über die Eigenschaften und die Einsetzbarkeit verschiedener Rechnerarchitekturen werden u.a. Thema der im Rahmen des Lehrgangs stattfindenden Computerdemonstrationen sein.
Der Kurzlehrgang wendet sich an all diejenigen, die selbst
Rechenprogramme für Strömungssimulationen entwickeln oder aber
kommerzielle Softwarepakete anwenden. Programmentwickler finden durch
die detaillierte Behandlung aller Einzelschritte, die zur
Programmerstellung notwendig sind, wertvolle Unterstützung. Anwender
haben die Gelegenheit, die wesentlichen Bestandteile eines kompletten
Berechnungsverfahrens und dessen Funktionsweise kennenzulernen; dies
ist sowohl für die Anwendung als auch für die kritische
Interpretation der Ergebnisse von Softwarepaketen unverzichtbar.
Besonders nützlich und reizvoll für alle Teilnehmer sollte nicht
zuletzt die Möglichkeit sein, durch Diskussionen mit den Vortragenden
Informationen über die neuesten Entwicklungen auf dem Gebiet der
Numerischen Strömungsmechanik aus erster Hand zu bekommen. Weitere
Infos und Anmeldeformulare finden Sie auf der unten angegebenen
WEB-Page.
| Termin | 27.-30. März 2000 |
| Ort | LSTM Erlangen |
| Anmeldung | ab sofort (bis 1.2.2000 Preisnachlass) |
| Leitung | Dr.-Ing. M. Breuer |
| Dipl.-Phys. Frank Schäfer | |
| Dipl.-Ing. René Volkert | |
| numet2000@lstm.uni-erlangen.de | |
| URL | http://www.lstm.uni-erlangen.de/numet2000/ |
FORTWIHR Gäste
Bitte notieren: