
Nach so viel harscher Kritik am Zensor in den vergangenen Ausgaben des Quartls erscheint es nun als ein Gebot der Fairness, auch einmal seinen wissenschaftspolitischen Instinkt zu rühmen. Was ist geschehen? Im letzten Quartl, an ganz und gar unprominenter "Übrigens"-Stelle, war auf einen zensierten Beitrag mit dem Titel "Neuer Ärger mit den Preiß'n" hingewiesen worden, der die eine oder andere plötzliche und natürlich rein sachlich motivierte Kursänderung bei der Diskussion um Zukunft und Standorte der Bundeshöchstleistungsrechner in gewohnt unterwürfiger Art hätte kommentieren {s/w}ollen. Der Zensor legte jedoch sein Veto ein und bewies dabei untrügliches Gespür für Schlingerbewegungen. Deren (vorerst) letzte hatte nämlich Ende Januar (gerade 'mal einen Monat nach Erscheinen besagter Quartl-Ausgabe) dann doch noch für eine (aus bayerischer Sicht) positive Wendung gesorgt und mit dem Votum des Wissenschaftsrats für den Standort München bzw. für die bayerische Lösung ein versöhnliches Ende herbeigeführt. Nicht auszudenken, welch' Flurschaden durch übereilte und in der Sache dann schlussendlich gar nicht gerechtfertigte Polemik im Massenblatt Quartl angerichtet worden wäre! Womit wir bei der eigentlichen frohen Botschaft dieses Quartls wären: Der Bundesrechner kommt, und die Vorbereitungen für das flankierende Kompetenznetzwerk zum Hochleistungsrechnen in Bayern laufen bereits auf vollen Touren. Folgerichtig lassen wir die Brust anschwellen und stimmen alle ein in ein nicht zu überhörendes "Vivat!" - auf unseren Zensor, auf unsere bayerische Obrigkeit, auf den Wissenschaftsrat, und überhaupt.

Wer nun aber geglaubt oder gehofft hatte, damit sei der Ärger mit den Preiß'n vom Tisch, der sah sich zwei Tage später getäuscht, ins bayerische Mark getroffen und in seinen schlimmsten Vorurteilen bestätigt. Allen Abrüstungsbemühungen zum Trotz feuerte das in Berlin ansässige Bundesverwaltungsgericht mit Mehrfach-Sprengköpfen bestückte Raketen gen Süden ab, mitten ins Herz, in unsere Biergärten. "Ein bayerisches Anliegen und Berliner Richter - da muss ja eine preußische Bosheit 'rauskommen", jammerten in der AZ die, die's schon seit anno Bismarck immer gewusst hatten. Linke und Rechte, Fundis und Realos, Papisten und Lutherische, Müsli-Jünger und Fleischfresser, Asketen und Trinkfeste, alle waren und sind sich einig, dass man sich im Süden eine derartige Dreistheit nicht bieten lassen könne. Also übergeben die Verfechter effizienter Rechenart die Stafette bzw. den Fehdehandschuh an die Verfechter bodenständiger Lebensart, und der ewige Kampf geht weiter.
So gut versteckt war oben erwähnter Hinweis auf den (jetzt wohl definitiv nie erscheinenden) Beitrag übrigens doch nicht, fühlte sich einer unserer treuesten Leser aus den preußischen Kernlanden doch sogleich zu einem Leserbrief animiert. Sehr zu unserer Enttäuschung blieb es dann aber doch bei der Ankündigung dieses (in mundartlicher Aufbereitung avisierten) ersten externen Beitrags - hoffentlich nicht allein aufgrund unserer Vorbehalte gegen einen "Abdruck-Persilschein". Schließlich gehört es zum Wesen der Zensur, vor Drucklegung zu zensieren, aber vielleicht sieht man das im liberalen und aufgeklärten Preußen ja etwas anders.
Abschließend noch ein Nachtrag zum letzten Editorial. Dort war versprochen worden, die Leserschaft des Quartls bzgl. der weiteren Entwicklung an der Namensgebungsfront auf dem Laufenden zu halten, was hiermit auch geschehen soll. Um es kurz zu machen: "FORTWIHR" ist vom Tisch, "FORTWIHR III" ebenfalls, and the winner is: "FORTWIHR (III)" (in Worten: FORTWIHR - Klammer auf - III - Klammer zu). Ein salomonischer Kompromiss, der die Symbiose aus Kontinuität und Neuanfang geradezu perfekt zum Ausdruck bringt.
Somit bleibt mir nur noch, auf die diesmal hinsichtlich Anzahl, Umfang und Inhalt erfreulichen Beiträge aus dem FORTWIHR hinzuweisen, die ohne Mitwirkung der Redaktion entstanden sind. Nur gute Vorsätze für die Fastenzeit oder am Ende gar eine Trendwende?
"I am an old man now, and when I die and go to heaven (also ein Optimist!) there are two matters on which I hope for enlightment. One is quantum electrodynamics, and the other is the turbulent motion of fluids. And about the former I am rather optimistic (1932)."
Na klar, Akte X trägt die Aufschrift "Turbulenz", und niemand kann sich ihr entziehen, da sie im wahrsten Sinne des Wortes auch in uns ist, z.B. im Blutkreislauf oder in den Atemwegen. Aber sie begegnet uns auch ständig im Alltag. Jeder kennt wohl das Phänomen, dass sich der glatte Wasserstrahl plötzlich kräuselt, wenn man den Hahn weiter aufdreht, oder der aufsteigende Qualm einer Zigarette eine scheinbar völlig ungeordnete Struktur annimmt. Beides sind turbulente Strömungsphänomene.
In der Technik sind praktisch alle Strömungen turbulent - hier sind turbulente Strömungen die Regel, nicht die Ausnahme. Wenn man nur mal exemplarisch an unsere modernen Fortbewegungsmittel wie Auto, Zug oder Flugzeug denkt, so werden alle turbulent umströmt, was sich leider i.a. widerstandserhöhend auswirkt. So könnten z.B. allein im Luftverkehr jedes Jahr Millionen Liter Treibstoff eingespart werden, wenn es gelingen würde, die Strömung um das Flugzeug auch nur teilweise laminar zu halten - eine Thematik, an der übrigens schon seit längerem gearbeitet wird. Aber die Turbulenz hat nicht nur negative Auswirkungen wie die erwähnte Widerstandserhöhung. In bestimmten Anwendungen kann man die Eigenschaften turbulenter Strömungen auch technisch ausnutzen. Dies geschieht z.B. in Triebwerksbrennkammern, in denen die Turbulenz zu einer besseren Vermischung der Luft mit dem Treibstoff und somit zu einer effizienteren Verbrennung führt.
Die Liste der in der Natur und Technik zu beobachteten turbulenten
Strömungsphänomene ist lang, und die von ihr ausgehende
Faszination/Anziehungskraft für Naturwissenschaftler und Ingenieure
ist verständlich. Der Wunsch, turbulente Strömungen berechnen zu können,
ist schon sehr alt, aber dennoch nur in Ansätzen in Erfüllung gegangen.

Warum ?
Um dies zu verstehen, muss man sich eine
turbulente Strömung mal genauer ansehen. Ein russischer
Wissenschaftler namens Kolmogorov hat dazu bereits 1941 ein sehr
anschauliches Modell aufgestellt. Er entwickelte die Idee, das
chaotische Verhalten einer turbulenten Strömung durch eine
Überlagerung von Wirbeln unterschiedlicher Größenordnungen zu
beschreiben. Die größten Wirbel haben dabei die Abmessung des
umströmten Körpers. Die kleinsten Elemente ergeben sich aus dem
Energiehaushalt des Systems. Dabei nimmt man an, daß die Zufuhr der
Energie über die großen Wirbel erfolgt, die diese Energie jedoch
nicht behalten, sondern in Form eines Kaskadenprozesses an die
Elemente der nächst kleineren Größenordnung abgeben. Das Ende der
Energiekaskade ist erreicht, wenn die zugeführte Energie in den
kleinsten Wirbeln durch die Wirkung der viskosen Kräfte in Wärme
dissipiert wird. Nach Kolmogorov wird das Verhältnis der großen zu
den kleinsten Wirbeln durch die Reynoldszahl Re(3/4)
(Reynoldszahl Re = Verhältnis von Trägheits- zu viskosen Kräften) bestimmt.
Diese Beziehung kann dazu genutzt werden, den Aufwand für die Berechnung einer turbulenten Strömung mittels sogenannter Direkter Numerischer Simulation (DNS) abzuschätzen. Da Turbulenz immer dreidimensional ist, braucht man zu ihrer Berechnung ein numerisches Gitter, dessen Gitterpunktanzahl mit Re(3/4) * 3 ansteigt. Bedenkt man noch, daß turbulente Strömungen auch immer zeitabhängig sind, wächst der numerische Simulationsaufwand sogar mit Re(11/4) an. Mit den heutigen Superrechnern kommt man damit zu Reynoldszahlen in der Größenordnung 104. Dumm ist nur, dass bei den meisten technischen Anwendungen viel größere Reynoldszahlen auftreten, beim obigen Beispiel des Verkehrsflugzeuges z.B. Re ~ 108. Um also die Strömung um ein komplettes Flugzeug mittels DNS berechnen zu können, braucht man ein "Superhirn", das 1011 mal schneller ist als das, was uns heute im Idealfall zur Verfügung steht, d.h. eine Leistung von 1023 Flop/s. (Dies ist durch das einfache Zusammenlöten vieler PC-Prozessoren übrigens nicht zu erreichen!) Dieses Superhirn würde dann immer noch ziemlich lange beschäftigt sein, um am Ende "die Antwort auf die Frage aller Fragen" (hoffentlich nicht 42!) auszuspucken.
Darauf woll(t)en (ungeduldige) Ingenieure und Physiker aber nicht warten und haben sich einen Ausweg ausgedacht, die sogenannte Reynolds-gemittelte Betrachtungsweise (RANS) bzw. die Large-Eddy-Simulation (LES). Verzichtet man darauf, alle Skalen des turbulenten Strömungsfeldes zu berechnen, weil man z.B. nur an den Mittelwerten der Strömung interessiert ist, kann man die Erhaltungsgleichungen in der Zeit (RANS) bzw. im Raum (LES) mitteln und nur diese numerisch lösen, was einen um Größenordnungen kleineren Aufwand hervorruft. Von dieser List des Menschen erzürnt, haben die "Götter der Turbulenz" dem Vorgehen allerdings einen schweren Balken vorgeschoben, den sogenannten Reynoldsschen Spannungstensor. Dieser entsteht bei der Mittelung der Erhaltungsgleichungen und kann nicht direkt berechnet werden. Der Ausweg sind sogenannte Turbulenz- bzw. Feinstrukturmodelle, von denen es Varianten in allen denkbaren Komplexitätsgraden gibt, angefangen bei einfachen algebraischen Beziehungen (wie z.B. dem Prandtlschen Mischungswegansatz) bis hin zu den komplexen Reynoldsspannungsmodellen. In all diesen Modellen stecken eine Reihe von freien Parametern drin, die man zwar anhand von geeigneten Testfällen kalibrieren kann, die aber gleichzeitig auch die Allgemeingültigkeit in Frage stellen. Das eigentliche Dilemma besteht darin, dass die Modelle und die in ihnen getroffenen Annahmen nur so gut sein können wie das physikalische Verständnis, das man über die komplexen Vorgänge innerhalb einer turbulenten Strömung hat. Trotz bereits langjähriger Forschungsarbeiten (leider zum größten Teil in den USA) ist ein echter Durchbruch bisher nicht gelungen.
Dabei stellt die Tatsache, dass die meisten praxisrelevanten Rührwerksströmungen turbulent, dreidimensional und zeitabhängig sind, hohe Anforderungen an die Modellierungsstrategie und die Computerressourcen. Des weiteren können die numerischen Methoden nur gemeinsam mit experimentellen Strömungsuntersuchungen entwickelt werden, da diese zur Validierung der Berechnungen und zur Verbesserung der Turbulenzmodelle herangezogen werden müssen. Am LSTM-Erlangen werden daher kombinierte experimentelle und numerische Methoden für die Berechnung einphasiger Strömungen in gerührten Behältern eingesetzt.
In jüngster Vergangenheit konzentrierte sich die numerische Simulation (CFD = Computational Fluid Dynamics) von Rührwerksströmungen auf die Berechnung des großräumigen Geschwindigkeitsfeldes. Während die Geschwindigkeitsfelder sowohl qualitativ als auch quantitativ mit ausreichender Genauigkeit erfasst werden konnten, wurden die turbulenten Größen in der Simulation zu niedrig vorhergesagt. Bedenkt man, dass der Turbulenz in vielen Rühr- und Mischprozessen, wie z.B. bei Dispergiervorgängen und mikromischbeieinflussten chemischen Reaktionen, eine entscheidende Bedeutung zukommt, besteht ein dringender Bedarf darin zu klären, wieso die verwendeten Turbulenzmodelle zu den unbefriedigenden Ergebnissen bei der Berechnung der turbulenten kinetischen Energie führen. Einige Forschungsgruppen führten dieses auf die Anisotropie der Strömung zurück, die bei den verwendeten Standard k-e-Modellen nicht berücksichtigt werden kann.
Hierauf aufbauend wurden am LSTM-Erlangen im Rahmen eines EU-Projektes ("Chemical Reactor Simulation for Fast Exothermic and Mixing Sensitive Reactions") detaillierte Untersuchungen zur Leistungsfähigkeit des Standard k-e-Modells durchgeführt. Bei sehr feinen Gittern können Turbulenzwerte vorhergesagt werden, die mit den Ergebnissen aus LDA-Messungen in sehr guter Übereinstimmung sind. Insbesondere ist eine Verfeinerung des Gitters in Nähe der Rührelemente erforderlich, so dass wichtige Strömungsvorgänge wie die Ausbildung von Ablösewirbeln erfasst werden können. Die Abbildungen illustrieren das simulierte Strömungsfeld in der Nähe der Rührblätter eines Schrägblattrührers im Vergleich zu den Ergebnissen von LDA-Messungen.
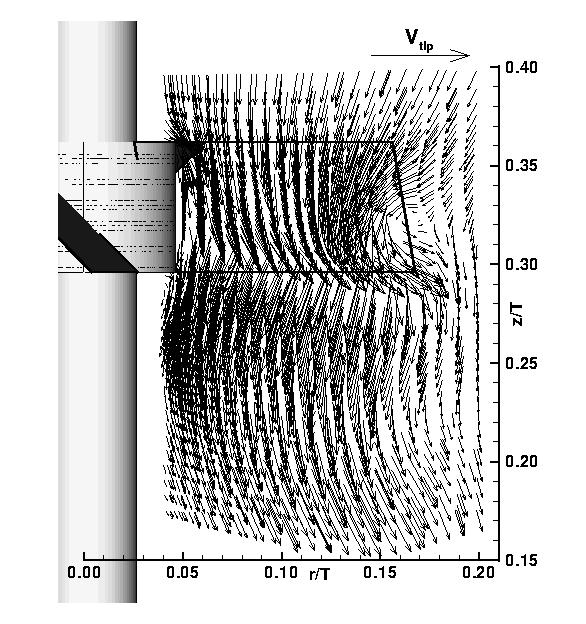
|
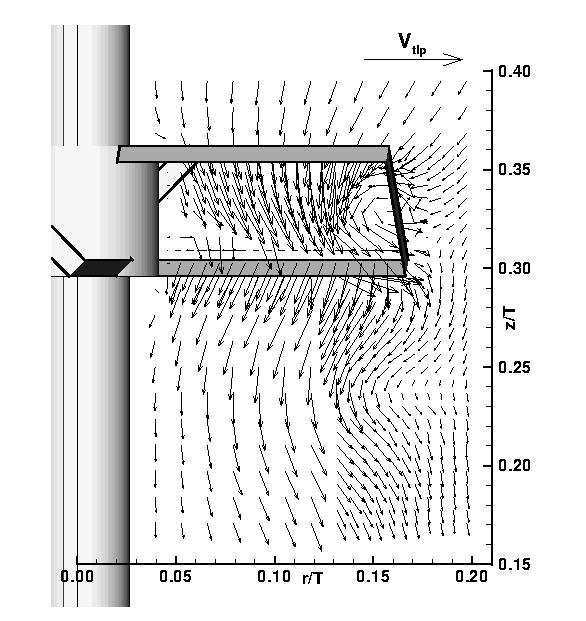
| |
| Strömungsfeld aus Simulation | Strömungsfeld aus LDA-Messungen |
Die Ergebnisse zeigen auf, dass es mit Hilfe moderner numerischer Methoden möglich ist, realistische Vorhersagen der Strömungsvorgänge innerhalb des gesamten Rührbehälters zu treffen. Damit konnte ein wichtiger Beitrag zu einer besseren Auslegung von Rühr- und Mischprozessen mit Hilfe von Simulationsprogrammen geleistet werden.
Seit 5 Jahren fördert das Bundesministerium für Bildung und Forschung (BMBF) mit rund 7 Millionen Mark jährlich 60 mathematische Forschungsgruppen an deutschen Hochschulen, die in direkter Kooperation mit Industriepartnern an der Lösung drängender technischer und wirtschaftlicher Probleme arbeiten. Der Bogen der Aktivitäten reicht dabei von der Medizin (z.B. Verbesserung und neue Einsatzmöglichkeiten der Computertomographie) über die Mikroelektronik (z.B. Entwicklung leistungsfähigerer Halbleiterbauelemente) bis hin zur optimalen Verkehrsführung (z.B., um Staus auf Autobahnen zu vermeiden).
Im Hintergrund steht dabei die Einsicht, dass ein rohstoffarmes Land wie Deutschland künftig verstärkt seine Möglichkeiten nutzen muss, die durch innovative Forschung im Hochtechnologiebereich geboten werden. Der modernen Mathematik fällt dabei in vielen technisch-wissenschaftlichen Bereichen die Rolle einer Schlüsseltechnologie zu. Neueste algorithmische Verfahren erlauben heute im Verbund mit moderner Computertechnologie die mathematische Modellierung selbst komplexer technischer Vorgänge und ihre anschließende Simulation auf dem Rechner. So können extrem zeitaufwendige und kostspielige Experimente eingespart oder sogar ganz ersetzt werden. Man denke etwa an die Untersuchung des Fahrverhaltens von (noch nicht gebauten) Autoprototypen oder an die Entwicklung einer neuen Generation von Großraumflugzeugen, die im Experiment gar nicht möglich ist. So gewonnene Erkenntnisse fließen häufig direkt in neue Konstruktionsverfahren ein.
Die Universität Erlangen-Nürnberg ist über die Lehrstühle für Angewandte Mathematik (Prof. Dr. P. Knabner und Prof. Dr. J. Zowe) mit 2 Projekten an dem BMBF-Vorhaben beteiligt. Die Gruppe um Prof. Knabner modelliert und simuliert den Fluidtransport und chemische Reaktionen in porösen Medien, z.B. im Erdreich. Eines der Ziele ist der Entwurf und die Analyse neuer Sanierungstechnologien mit dem Einsatz von Tensiden für schadstoffbelastete Böden. Die Mitarbeiter von Prof. Zowe arbeiten zusammen mit der DASA an der optimalen Auslegung von Stabwerken wie Brücken oder Elektrizitätsmasten sowie an Modellen zur Konstruktion und Optimierung neuer Verbundwerkstoffe, wie sie z.B. in der nächsten Flugzeuggeneration Verwendung finden sollen. Zusammen mit der Siemens AG Erlangen richteten die beiden Lehrstühle das Treffen aller vom BMBF geförderten Projektgruppen aus, das vom 17. - 19. Februar in Erlangen stattfand.
An FORTWIHR-Mitgliedern sind außer Prof. Knabner auch die Profs. Bulirsch, Hoffmann, Hoppe und Müller als Projektleiter an den BMBF-Projekten beteiligt. Ohne die Unterstützung von Seiten der Siemens AG in Person von Prof. Gilg und Dr. Maurer als lokalem Organisator wäre der reibungslose Ablauf der Tagung nicht möglich gewesen.
Einen exemplarischen Eindruck von den Chancen, aber auch Grenzen der modernen Mathematik im Bereich der Hochtechnologie gab der öffentliche Abendvortrag von Prof. Dr. P. Deuflhard. Der Präsident des Konrad-Zuse-Zentrums für Informationstechnik in Berlin befasst sich im Rahmen eines Projektes mit der Zerstörung menschlicher Krebszellen durch Überwärmung. Wo und wie hier Mathematik zum Tragen kommt, stellte er in seinem Vortrag "Mathematik im Dienste der Krebsmedizin: Optimale Therapieplanung am virtuellen Patienten" dar, der sich auch an mathematische Laien wandte.
"Die Berechnung der Flugbahn eines Satelliten ist ein klassisches Problem, man will mit möglichst wenig Treibstoff das Ziel erreichen und lieber mehr Nutzlast mitnehmen."
Rainer Callies, Akademischer Rat am Lehrstuhl M2 "Numerische Mathematik" des Zentrums Mathematik der TUM, entwickelte zur präzisen Optimierung kompliziertester Flugbahnen neue Algorithmen für Hochleistungscomputer. Bei seinen Berechnungen bezog er auch Anforderungen wie Flugzeit-Limit, maximale Beschleunigung, Aufheizung oder die Störkräfte von Planeten und Monden mit ein. "Diese Probleme lassen sich mathematisch als komplexe Systeme hoch-nichtlinearer Differentialgleichungen formulieren, lösen lassen sie sich mit den Mitteln der klassischen nichtnumerischen Mathematik nicht mehr."
Er berechnete mit dem Werkzeug Computer die Flugbahnen. "Doch das ist nur der Anfang. Immer präzisere Optimierungstechniken gestatten es, in den Konstruktionsprozess der Raumsonde selbst einzugreifen. Das Fachwissen des Ingenieurs wird für den Computer aufbereitet und in mathematische Formalismen eingebettet." Im Zusammenspiel beider Fächer entstehen im Rechner Konzepte für neue Raumflugkörper. Callies entwickelte für die Berechnungen neue mathematische Verfahren und "schickte" Raumsonden zu Asteroiden und eine Miniatursonde zum Planeten Venus, auch Testflugbahnen für Überschallflugzeuge hat er berechnet.
Die Optimierungsmethoden aus der Raumfahrt überträgt Callies inzwischen auch in Konzepte zur computergestützten Chirurgie: "Die Hand des Chirurgen, der sein Operationswerkzeug führt, lässt sich mit Gleichungen ebenso beschreiben wie der Schwerpunkt einer Rakete." Wobei er die abstrakten Inhalte auch computergrafisch neu visualisiert.
Mathematik, wie Callies sie betreibt, ist also alles andere als ein nüchternes Zahlenspiel. Dass er ein Doppelstudium in Mathe und Physik absolvierte, hat ihm sehr geholfen: "An den Grenzflächen der Fächer liegt sehr viel Neuland", betont er.
Ferienakademie 1999 | |
|---|---|
Das diesjährige Programm der Ferienakademie der Universität Erlangen-Nürnberg und der TU München im Sarntal, 19.9. - 1.10.1999: |
|
| 1. Daten- und Wissensbanken | Prof. R. Bayer (TUM), Prof. H. Stoyan (FAU) |
| 2. Bäume - Algorithmik und Kombinatorik | Prof. E. W. Mayr (TUM), Prof. V. Strehl (FAU) |
| 3. Kräfte und Felder | Prof. F. von Feilitzsch (TUM), Prof. C. Toepffer (FAU) |
| 4. Moderne Verbrennungstechnik: Grundlagen und aktuelle Problemstellungen | Prof. A. Leipertz (FAU), Prof. T. Sattelmayer (TUM) |
| 5. Intelligente Makromolekulare Systeme: Synthese, Struktur, Funktion | Prof. A. Hirsch (FAU), Prof. O. Nuyken (TUM) |
| 6. Risikomanagement in der Finanzindustrie | Prof. C. Klüppelberg (TUM), Prof. B. Rudolph (LMU München) |
| 7. Breitbandige Übertragungsverfahren in der Mobilkommunikation | Prof. J. Hagenauer (TUM), Prof. J. Huber (FAU) |
| 8. Physikalische Grundlagen der Halbleiterelektronik | Prof. G. Döhler (FAU), Prof. F. Koch (TUM) |
| 9. Numerische Methoden in der Fluid- und Strukturmechanik | Prof. F. Durst (FAU), Prof. E. Rank (TUM) |
| 10. Ethik der Technik: Selbstverständnis und Verantwortung beim Gestalten von Technik | Prof. H. G. Ulrich (FAU), Prof. U. Wengenroth (Münchner Zentrum für Wissenschafts- und Technikgeschichte) |
| 11. Erweiterte Realität: Bildbasierte Modellierung und tragbare Computer | Prof. B. Brügge (TUM), Prof. H. Niemann (FAU) |
| Anmeldeformulare und nähere Informationen gibt es hier: http://www5.in.tum.de/FA/ | |
FORTWIHR Intern
FORTWIHR Vorträge
FORTWIHR Gäste
Bitte notieren:
Übrigens...