Bachelor-Praktikum: Tsunami-Simulation - Summer 13

From Sccswiki
Jump to navigation Jump to search
Term
SS 13
Lecturer
Univ.-Prof. Dr. Michael Bader,
Alexander Breuer,
Sebastian Rettenberger
Time and Place
Monday 16:00-18:00, lecture room MI 02.07.023
Audience
Studenten der Informatik (Bachelor)
(Module IN0012)
Tutorials
-
Exam
-
Semesterwochenstunden / ECTS Credits
6 SWS (6P) / 10 Credits
TUMonline
https://campus.tum.de/tumonline/lv.detail?clvnr=950099139



Description

In this lab course we systematically address modern software engineering approaches in an application driven context: Tsunami simulations. Starting from implementation of a solver in a one dimensional setting, the complete process over integration in an existing framework to optimization and parallelization is covered. During this process key issues of software engineering are dealt with: versioning, documentation, unit testing, file I/O, ..

During the course, assignments are to be solved by groups of three participants each followed by presentations in regular meetings. A project phase with individual study projects chosen by the groups completes the lab course.

Requirements

  • Knowledge of object oriented programming
  • Basic knowledge of C or C++
  • Interest in a challenging but exciting topic

The spoken language in the meetings is German, slides and assignments are in English.

Timeline

Examples

Lab swe.png

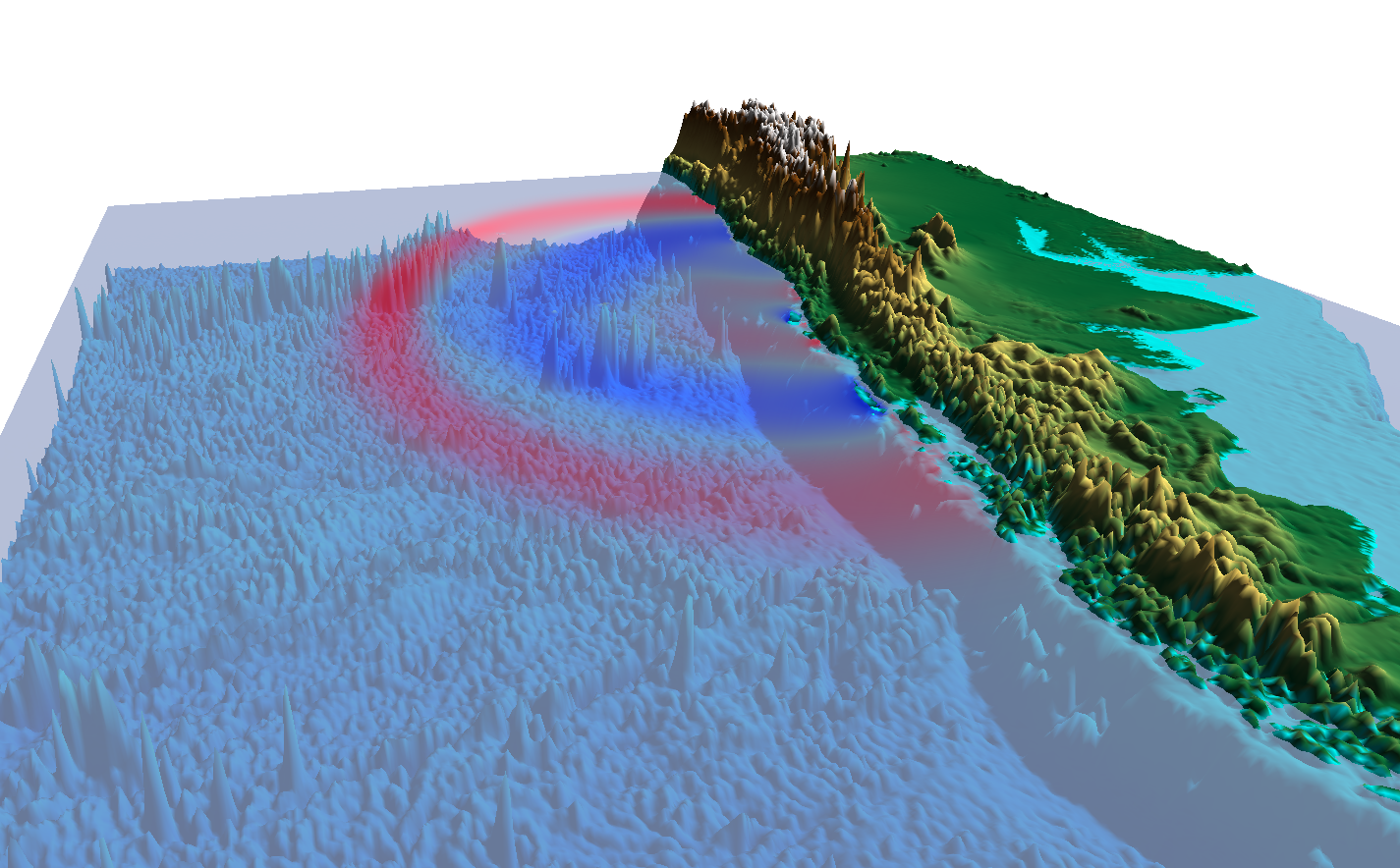
Live visualization of the February 2010 Chilean tsunami using OpenGL.

Lab tohoko overview.png

Propagation of the 2011 Tohoku tsunami.

Lab tohoko coast.png

Run-up of the 2011 Tohoku tsunami.

Lab tohoku field.png

Dart station comparison of the 2011 Tohoku tsunami.

Lab godunov step.png

Sketch of the Finite Volume method with shock waves arising in the Riemann solutions.

Retrieved from "https://www5.in.tum.de/wiki/index.php?title=Bachelor-Praktikum:_Tsunami-Simulation_-_Summer_13&oldid=13317"